Задачи - УПП, Седмица 4, 23.10.2025
GitHub Classroom: https://classroom.github.com/a/rOzekyCs
За решаване
Задача 1
От входа получавате две реални числа. Трябва да ги върнете в нарастващ ред.
| Вход | Изход |
|---|---|
| 8 7 | 7 8 |
| 2.6 11.991 | 2.6 11.991 |
| -2.5 -11.1 | -11.1 -2.5 |
Задача 2
От входа получавате буква. Трябва да изкрате:
- "Lowercase letter" ако е малка буква,
- "Uppercase letter" ако е главна буква,
- "Digit" ако е цифра и
- "Other" в останалите случаи.
| Вход | Изход |
|---|---|
| k | Lowercase letter |
| Q | Uppercase letter |
| 8 | Digit |
| + | Other |
Задача 3
От входа получавате ден в месеца (допускаме 30-дневен месец, където първи ден е Понеделник; като месец Септември от тази година). Трябва да върнете името на деня от седмицата.
| Вход | Изход |
|---|---|
| 2 | Tuesday |
| 7 | Sunday |
| 8 | Monday |
| 19 | Friday |
| 30 | Tuesday |
Задача 4
От входа получавате реални коефициенти на квадратно уравнение: a, b и c.
Трябва да изкарате корените на уравнението, като:
- ако има два корена, изкарвате и двата,
- ако има един корен, изкарвате само него,
- ако няма реални корени, изкарвате "No real roots".
| Вход | Изход |
|---|---|
| 5 6 1 | -0.2 -1 |
| 5 2 1 | No real roots |
| 4 -12 9 | 1.5 |
Задача 5
От входа получавате буква, съответстваща на операция върху числа:
-
_за закръгляне надолу на число -
+за събиране на две числа -
*за умножение на две числа -
xза умножение на три числа -
.за умножение на четири числа
След тази буква ще получите съответния брой реални числа и трябва да изкарате резултата от операцията.
| Вход | Изход |
|---|---|
| _ 5.7 | 5 |
| + 9 10 | 19 |
| * 2 2 | 4 |
| x 2 2 3 | 12 |
| . 8 -2 0.5 | -8 |
Задача 6
От входа получавате число, което определя фигура. Това число може да бъде:
-
1за окръжност, -
2за правоъгълник и -
3за триъгълник.
Спрямо типа фигура, ще приемете различен брой реални числа:
- за окръжност - радиус,
- за правоъгълник - дължините на двете (уникални) страни,
- за триъгълник - дължините на трите страни.
Използвайки тези числа, трябва да изкарате периметър (дължина) на фигурата. За константата π използвайте поне 5 цифри след запетаята.
| Вход | Изход |
|---|---|
| 1 38.1 | 239.389 |
| 2 70 25 | 190 |
| 3 1000 238.5 611.13 | 1849.63 |
Задача 7
От входа получавате цяло число. Изкарайте за него таблицата на умножение от 1 до 10 включително.
Използвайте цикъл!
| Вход | Изход |
|---|---|
| 7 |
|
| -8 |
|
Задача 8
От входа получавате две цели положителни числа, a и x.
Пресметнете a на степен x.
| Вход | Изход |
|---|---|
| 2 8 | 256 |
| 1 100 | 1 |
| 83 1 | 83 |
| 61 5 | 844596301 |
Задача 9
От входа получавате цяло положително число. Трябва поотделно да сумирате всички четни и нечетни числа от 1 до подаденото число, включително. Накрая изкарайте двете суми.
| Вход | Изход |
|---|---|
| 10 | 30 25 |
| 1 | 0 1 |
| 64 | 1056 1024 |
Задача 10
От входа получавате цяло положително число. Изкарайте за него "Prime" ако е просто и "Not prime" ако не е, последвано от най-малкия делител (различен от 1 и самото число).
| Вход | Изход |
|---|---|
| 2 | Prime |
| 4 | Not prime 2 |
| 3313 | Prime |
| 1408969 | Not prime 1187 |
Задача 11
От входа получавате цели числа докато не срещнете числото 0. Трябва да върнете умножението на всички тези числа (без нулата).
| Вход | Изход |
|---|---|
| 1 2 3 0 | 6 |
| -10 15 6 -3 7 0 | 18900 |
| -4 -50 58 9 -25 -7 -3 27 0 | -1479870000 |
Задача 12
От входа получавате знак.
Ако този знак е аритметична операция (+, -, *, /), тогава ще получите две цели числа.
Трябва да пресметнете резултата на операцията върху тези числа, да го изкарате и пак да очаквате знак.
Ако този знак е точка, тогава спирате програмата.
При вас вход и изход ще са смесени.
| Вход | Изход |
|---|---|
| + 8 4 - 10 5 . | 12 5 |
| . | |
| * 64 128 / 100 20 * 7 7 + 90 10 . | 8192 5 49 100 |
Задача 13
Редицата на Фибоначи е последователност от числа, където всяко следващо е равно на сумата на предходните две. По-точно, първото число (на индекс 0) е 0, второто число (на индекс 1) е 1 и всяко следващо се определя от предходните две.
От входа получавате неотрицателен индекс и трябва да изкарате съответното число на фибоначи.
| Вход | Изход |
|---|---|
| 5 | 5 |
| 6 | 8 |
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 12 | 144 |
| 33 | 3524578 |
Задача 14
От входа получавате цяло неотрицателно число. Трябва да обърнете реда на цифрите в числото и да изкарате резултата.
| Вход | Изход |
|---|---|
| 123 | 321 |
| 500 | 5 |
| 1002 | 2001 |
| 27644437 | 73444672 |
За самоподготовка
Задача 15
Получавате реално число: оценка по шестобалната система. Трябва да върнете "наименованието" на оценката спрямо стойността:
- "Excellent" (за 5.5 или повече),
- "Very good",
- "Good",
- "Average",
- "Weak" (оценки от 2.99 до 2.0) и
- "Bad" (по-малко от двойка)
| Вход | Изход |
|---|---|
| 5 | Very good |
| 7.1 | Excellent |
| 3.5 | Good |
| 3 | Average |
| 2.8 | Weak |
| 1.9 | Bad |
Задача 16
Получавате три реални числа: ъгли в градуси. Трябва да върнете дали триъгълник с тези ъгли може да съществува, и ако да, дали е:
- равностранен ("Equilateral"),
- равнобедрен ("Isosceles"),
- остър ("Acute"),
- тъп ("Obtuse") или
- правоъгълен ("Right").
| Вход | Изход |
|---|---|
| 60 60 60 | Equilateral triangle |
| 30 120 30 | Isosceles triangle |
| 75 25 80 | Acute triangle |
| 90 60 30 | Right triangle |
| 107 33 40 | Obtuse triangle |
Задача 17
Факториел е функция върху число, която представлява умножението на всички цели числа от 1 до самото число включително.
От входа получавате цяло положително число. Трябва да изкарате неговия факториел.
| Вход | Изход |
|---|---|
| 5 | 120 |
| 1 | 1 |
| 2 | 2 |
| 9 | 362880 |
| 3 | 6 |
Задача 18
Във вашата програма запазете цяла неотрицателна константа. От входа получавате цели неотрицателни числа: опити да се познае.
Ако подаденото число е по-малко, трябва да върнете "Higher". Ако е по-голямо, трябва да върнете "Lower". Ако бъде познато, трябва да върнете "You guessed it!" и да спрете програмата.
В следните примери числото е 1337. Вашия вход и изход ще бъдат смесени.
| Вход | Изход |
|---|---|
|
|
Задача 19
Хармоничния ред е редица числа, където n-тото число се определя по формулата:
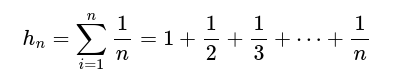
От входа ще получите положително цяло число n, трябва да върнете n-тото число в хармоничния ред.
| Вход | Изход |
|---|---|
| 1 | 1 |
| 2 | 1.5 |
| 5 | 2.28333 |
| 13 | 3.18013 |
| 20 | 3.59774 |
Задача 20
От входа получавате реално ненулево "целево" число и реално "обсег" число (в проценти). След това получавате редица реални ненулеви числа.
Продължавате да приемате реални числа, докато сумата на всички числа в редицата не е поне с "обсег" процента близкост до целевото число. Накрая на програмата изкарайте тази сума.
Формулата за процентова разлика между числа а и b е:
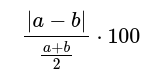
| Вход | Изход |
|---|---|
| 5 80 4.5 | 4.5 |
| 5 80 3 1.2 | 4.2 |
| 71.12 95.9 8 13 -5.5 21.9 -6 -1 42 | 72.4 |
| 50 1.5 20 | 20 |
За любознателните
Задача 21
В година 60та, преди близко до 2000 години, гръцкия математик Херон описва алгоритъм за пресмятане на корен квадратен на подадено число S. Описва се редица от числа x, където всяко следващо е равно на предходното, следвайки просто линейно взаимоотношение.
Всеки следващ член на редицата става все по-близък до истинската стойност на корена.
Първия член е произволно първоначално приближение. Разбира се, колко е по-близко приближението до истинската стойност, толкова по-бързо се приближаваме. Нека за нашите цели да използваме хиперболичното приближение.
Получавате цяло число S и индекс на член в редицата n. Трябва да върнете корена на числото по метода на Херон.
