Jump to content

Задачи - УПП, Седмица 13, 08.01.2026

important Използвайте рекурсия, за да решите всички тези задачи!

GitHub Classroom: https://classroom.github.com/a/8vTquPOY

За решаване

Задача 1

Реализирайте програма, която по подаден положителен размер изкарва "стълбище" от плюсове.

warn Както с всички останали задачи, решете условието с рекурсия!
Вход Изход
5 
+
++
+++
++++
+++++
2 
+
++
7 
+
++
+++
++++
+++++
++++++
+++++++

Задача 2

Припомняме, че в редицата на Фибоначи, всеки следвавщ елемент е сумата на предходните два, като първите два елемента са 0 и 1.

От входа получавате неотрицателен индекс, трябва да изкарате съответното число на Фибоначи.

warn Както с всички останали задачи, решете условието с рекурсия!
Вход Изход
5 5
6 8
0 0
1 1
2 1
12 144
33 3524578

Задача 3

От входа получавате цяло неотрицателно число. Изкарайте сумата на всички негови цифри.

warn Както с всички останали задачи, решете условието с рекурсия!
Вход Изход
123 6
1000 1
37581149 38

Задача 4

От входа получавате един ред с текст. Трябва да обърнете реда на всички букви в текста и да изкарате резултата.

Вход Изход 
Hello World

dlroW olleH

He should not have built the fire under the pine tree.

.eert enip eht rednu erif eht tliub evah ton dluohs eH

Задача 5

От входа получавате цяло неотрицателно число. Изкарайте "хълм" от плюсове с размер, подаденото число.

Вход Изход
4 
+
++
+++
++++
+++
++
+
2 
+
++
+
7 
+
++
+++
++++
+++++
++++++
+++++++
++++++
+++++
++++
+++
++
+

Задача 6

Напишете рекурентна функция, която по подадени две цели числа a и b, връща сумата и средното аритметично на всички числа между a и b, включително.

От входа получавате две цели числа. Използвайки вашата функция, изкарайте сумата и средното аритметично на всички цели числа в интервала [a, b].

Вход Изход
0 5 15 2.5
-8 14 69 3

Задача 7

От входа получавате неотрицателно цяло число - брой битове. Изкарайте всички възможни двоични числа, съставени от броя битове.

Вход Изход
2 
00
01
10
11
3 
000
001
010
011
100
101
110
111

Задача 8

От входа получавате неотрицателен индекс, трябва да изкарате преплетената поредица от числа на Фибоначи, от първото до това на подадения индекс. По-точно, трябва резултатните елементи на четните индекси да представляват редицата на Фибоначи в нарастващ ред, и тези на нечетните индекси да са същата редица в намаляващ ред.

warn Изполвайте само едно начално извикване на рекурентната ви функция.
Вход Изход
5 0 5 1 3 1 2 2 1 3 1 5 0
8 0 21 1 13 1 8 2 5 3 3 5 2 8 1 13 1 21 0
0 0 0

Задача 9

От входа получавате низ, съставен само и единствено от отварящи и затварящи кръгли скоби. Трябва да върнете дали скобите са балансирани, т.е. дали след всяка отваряща скоба, съществува "нейна си" затаваряща скоба, по-нататък в низа.

Вход Изход 
)()(
Not balanced 
(()(()((()(((())))()())))(()
Not balanced 
(((((((((((((())))))))))))))
Balanced 
()()()()()()()()()()()()()()
Balanced 
((()()((()()()())()))())((())()()()((())()(())))
Balanced

Задача 10

Използвайки опашкова рекурсия, имплементирайте функция която приема масив от реални числа и връща сумата на всички тях.

От входа получавате неотрицателно число N и след това N на брой реални числа. Използвайки вашата функция, изкарайте сумата на всички реални числа.

Вход Изход
5 1 2 3 4 5 15
9 8.3 5.1 90 45.44 19.99 -32 7 -2 0 141.83

Задача 11

Напишете програма, която решава пъзела с възрастта на трите деца. В пъзела знаете сумата на възрастите на трите деца, умножението на възрастите, както и факта, че едно от децата е най-голямо.

От входа получавате две положителни числа: сумата и произведението на възрастите. Трябва да изкарате резултата:

Вход Изход
14 72 3 3 8
13 36 2 2 9

Задача 12

От входа получавате неотрицателно число N и след това N на брой цели числа. Трябва да изкарате дължината на най-дългата нарастваща подредица (под-последователност) от числа.

Вход Изход
8 10 9 2 5 3 7 101 18 4
5 7 7 7 7 7 1
16 0 8 4 12 2 10 6 14 1 9 5 13 3 11 7 15 6

Задача 13

Напишете програма, която решава Такузу пъзели.

Пъзлите са формулирани така: в дъска 4 на 4 трябва да се попълнят нули и единици, така че на всяка колона и ред да има еднакъв брой нули и единици. Допълнително, на всеки ред и колона, не може да има повече от две последователни еднакви числа.

От входа получавате нерешен такузу пъзел, където "празните" позиции са маркирани с -1. Трябва да изкарате решение на пъзела.

Вход Изход 
-1  1 -1  0
-1 -1  0 -1
-1  0 -1 -1
 1  1 -1  0

0 1 1 0
1 0 0 1
0 0 1 1
1 1 0 0

-1  0  1 -1
 1 -1  0 -1
 0  1 -1 -1
 0  0  1 -1

1 0 1 0
1 1 0 0
0 1 0 1
0 0 1 1

-1  0 -1 -1
-1  0  0 -1
 0 -1 -1 -1
-1 -1 -1  0

0 0 1 1
1 0 0 1
0 1 1 0
1 1 0 0

За упражнение

Задача 14

Един от най-простите алгоритми за псевдо-случайни числа е генератора на Лемер. Започвайки от "seed" X0, всяко следващо случайно число Xk+1 е равно на (a * Xk) mod m, където а и m са константи.

Нека да фиксираме a = 16807 и m = 231 - 1. От входа получавате две положителни цели числа: "seed" и бройка N.

Трябва да изкарате всички произволни числа X1 до XN.

Вход Изход
1337 3 22470959 1859769514 521725159
0 5 0 0 0 0 0
1 5 16807 282475249 1622647863 947787490 1578127215

Задача 15

Във физиката, можем да определим позицията на едно тяло по елиптична (Кеплерова) орбита чрез екцентричната аномалия. Обаче, на практика тя не се намира директно, ами се изчисляват средната аномалия и ексцентрицитетът на елипсата.

Чрез уравнението на Кеплер, можем да изведем следната рекурентна връзка за екцентричната аномалия:

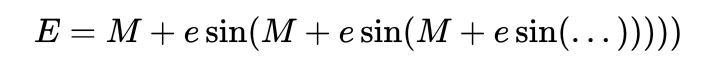
./img/eccentric-anomaly.png

Където M е средната аномалия и e е ексцентрицитетът на елипсата. От входа получавате две реални числа, M и e, както и цяло положително число "дълбочина". Трябва да върнете (приближение на) екцентричната аномалия, като рекурсията ви трябва да се "вложи" максимум "дълбочина" на брой пъти.

За дъно на рекурсията, може да върнете стойността M.

Вход Изход
10.831 5.2 4 9.36247
0 2 8 0
1 2 8 1.42528

Задача 16

От входа получавате две неотрицателни цели числа. Изкарайте техния най-голям общ делител, използвайки алгоритъма на Евклид:

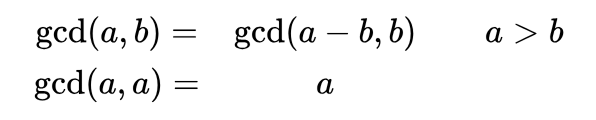
./img/gcd-euclid.png

Вход Изход
48 18 6
42 56 14
13 17 1

Задача 17

От входа получавате един ред с текст. Трябва да изкарате дали текста е палиндром.

Вход Изход 
Hello World
Not a palindrome 
racecar racecar
Is a palindrome

Задача 18

От входа получавате цяло неотрицателно число и цифра, между 1 и 9. Трябва да изкарате бройката срещания на цифрата в числото.

Вход Изход
1880 8 2
42 3 0
1111 1 4

Задача 19

Един от начините да изчислим стойността на биномен коефициент е чрез следната рекурентна връзка:

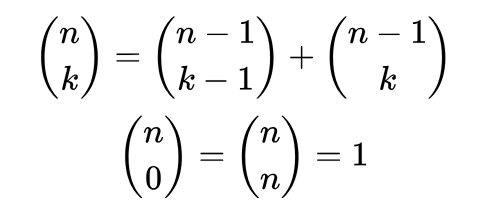
./img/binom.png

От входа получавате две неотрицателни цели числа n и k. Трябва да изкарате съответния биномен коефициент, използвайки рекурентната връзка.

Вход Изход
6 3 20
20 4 4845
9 9 1

Задача 20

Напишете програма, която "изиграва" всички възможни игри на морски шах и връща в колко тях някой печели и в колко от тях никой не печели.

Вход Изход
Wins: 209088 Draws: 46080

Задача 21

Разстоянието на Ливенщайн е метод за измерване на разликата между два низа. Смята се по следния начин:

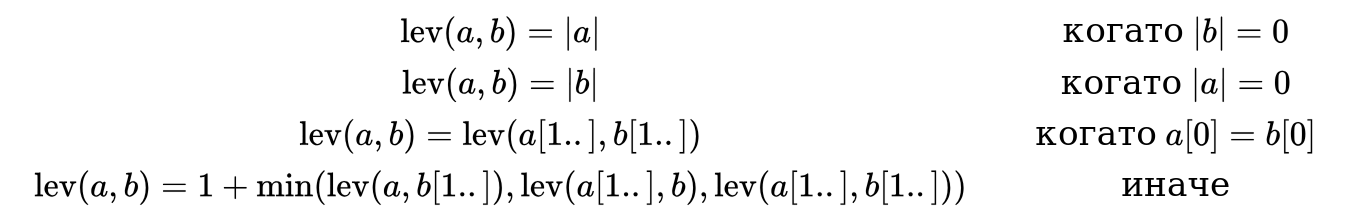
./img/levenshtein.png

Където с x[1..] бележим остатък от низа x, след първата буква.

От входа получавате два реда с текст. Трябва да върнете разстоянието на Ливенщайн между тях.

Вход Изход 
Hello
Harro
3 
World
World
0 
Winter land
Winterland
1

Задача 22

Аритметико-геометричното на две числа a и b се дефинира чрез следната рекурентна връзка:

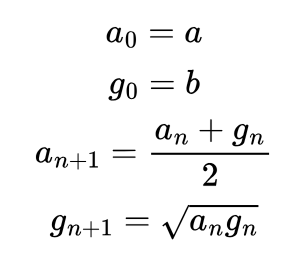
./img/agm.png

От входа получавате две реални числа, a и b, и брой итерации n. Изкарайте резултатното аритметико-геометрично число, като за дъно на рекурсията можете да върнете an+1.

Вход Изход
5 6 0 5.5
5 6 4 5.48861
0.18 0.2 8 0.189868

Задача 23

Използвайки опашкова рекурсия, напишете функция, която получава масив от цели числа и връща най-големия елемент от тях.

От входа получавате неотрицателно цяло N и след това N на брой цели числа. Използвайки вашата функция, изкарайте най-голямото число.

Вход Изход
5 -1 6 -2 9 0 9
6 1 1 1 1 1 1 1

Задача 24

Чрез бездънни дроби можем да представим редица функции/изрази, за които няма точна формула.

От входа получавате реално число x и дълбочина n, върнете ex използвайки:

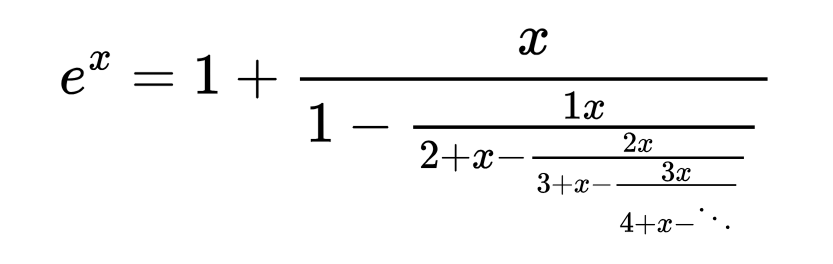
./img/eulers_identity.png

Като, всеки "етаж" от дробта е единица дълбочина (и първото ниво е 0).

Вход Изход
1 5 2.71667
1 10 2.71828
0.5 8 1.64872
3.14159 15 23.1406

Задача 25

От входа получавате положителни цели размери на матрица от букви. След това получавате стойностите на самата матрица, като буквата # определя стена и . определя празно пространство.

Накрая получавате двойка индекси (координат) в матрицата. Трябва да запълните всички празни клетки, които са достижими от подадения координат (като не може да се минаава през стените).

Задача 26

От входа получавате недовършен судоку пъзел, където празните клетки са отбелязани с -1. Трябва да намерите и изкарате решение(то) на пъзела.

Вход Изход 
 6 -1  3   2 -1  5   7 -1  1
-1  2 -1  -1 -1 -1  -1  9 -1
 9 -1 -1   6 -1  7  -1 -1  3

 1 -1  2  -1 -1 -1   6 -1  9
-1 -1 -1  -1 -1 -1  -1 -1 -1
 3 -1  5  -1 -1 -1   2 -1  7

 8 -1 -1   1 -1  6  -1 -1  2
-1  9 -1  -1 -1 -1  -1  5 -1
 7 -1  1   9 -1  2   3 -1  4


6 4 3  2 9 5  7 8 1
5 2 7  8 1 3  4 9 6
9 1 8  6 4 7  5 2 3

1 7 2  5 3 8  6 4 9
4 6 9  7 2 1  8 3 5
3 8 5  4 6 9  2 1 7

8 3 4  1 5 6  9 7 2
2 9 6  3 7 4  1 5 8
7 5 1  9 8 2  3 6 4

Задача 27

Редицата на Рекаман се дефинира по следния начин:

От входа получавате цяло неотрицателно чило n, изкарайте n-тото число от редицата на Рекаман.

Вход Изход
3 6
20 42
0 0
1 1

Задача 28

Напишете програма, която връща бройката решения на пъзела на 8те царици.

Пъзела е формулиран така: имате шахматна дъска (8 на 8) и върху нея имате 8 царици. Припомняме, че царицата се движи вертикално, хоризонтално и диагонално по дъската. Целта на пъзела е цариците да се поставят така, че нито една царица да не може да вземе никоя друга.

Вход Изход
92

Задача 29

От входа получавате положителни цели размери на матрица от букви. След това получавате стойностите на самата матрица, като буквата # определя стена и . определя празно пространство.

Накрая получавате две двойки координати (индекси) в матрицата. Трябва да изкарате дали има път по празните пространства, така че да се придвижите от началните (първите) координати до финалните (вторите).

Задача 30

От входа получавате два реда с текст. Първия ще наречем "регулярен израз", докато втория е подадения ни низ.

Регулярния израз представлява шаблон. Целта е да изкараме дали подадения низ съответства на шаблона.

За нашите цели, регулярнят израз ще има следния формат: започвайки от началото, всяка буква директно съответства на буква в подадения низ. Обаче, имаме специалната буква *, която казва, че предходната буква може да се повтори нула или повече пъти.

Тоест, ако в регулярния израз нямаме *, на практика проверяваме дали двата низа съвпадат. В случаите когато имаме *, пробваме да съпоставим буквата, например в регулярен израз "a*", низовете "", "a", "aa", "aaa" съответстват.

︽