Задачи - УПП, Седмица 8, 20.11.2025

GitHub Classroom: https://classroom.github.com/a/rhpKbNmH

За решаване

Задача 1

От входа получавате матрица 5 на 5 от цели числа. Трябва да върнете дали е разредена матрица: дали има повече нули отколкото други числа.

1 2 3 0 4
5 0 6 0 7
9 1 2 0 3
4 5 5 6 0
7 7 8 1 0

Not sparse

1 2 0 0 0
0 3 4 0 0
0 0 5 6 0
0 0 0 7 8
0 0 0 0 9

Sparse

Задача 2

Напишете функция, която получава матрица с произволен размер и масив, чиято дължина е същата като на един ред в матрицата.

Намерете сумата на всички редове и я запазете в подадения масив.

От входа получавате матрица 7 на 3 от цели неотрицателни числа. Използвайки вашата функция, намерете сумата на всички редове и я изкарайте.

79 23 76
71 50 41
 3 54  8
97 24  2
19 47 50
28 53 80
63 81 25

360 332 282

11 42 94
27 14 94
49 37 66
58 23 55
44 11 23
 3 77 31
12  4 16

204 208 379

Задача 3

Напишете функция, която получава две матрици с произволни размери, съствени от реални числа. Може да допуснете, че размера на втората матрица е по-малък от тази на първата.

Трябва да запишете във втората матрица, всички елементи от "горния ляв квадрат" на първата матрица. Тоест, всички елементи от горния ляв ъгъл, надолу и надясно колкото е размера на втората матрица.

От входа получавате матрица 6 на 6 от реални числа. След това получавате 4 реални числа: първите две са координат в матрицата (където горния ляв ъгъл е (0, 0)), вторите две са нейни размери.

Използвайки вашата функция, трябва да изкарате подматрицата с начало подадения координат и размери подадените размери използвайки вашата функция.

-10.181 15.910   0  78.309    192 59.743
 22.273 50.230 -82 -95.077      3      4
     10 45.834  -1   -0.02    5.5   18.2
 82.439  0.133 100      64 46.204  30812
    551    1.2 1.1  94.022  6.818     77
  8.608  10010   3   50.94  100.2 0.3333
0 0
6 6

-10.181 15.910 0 78.309 192 59.743
22.273 50.230 -82 -95.077 3 4
10 45.834 -1 -0.02 5.5 18.2
82.439 0.133 100 64 46.204 30812
551 1.2 1.1 94.022 6.818 77
8.608 10010 3 50.94 100.2 0.3333

-10.181 15.910   0  78.309    192 59.743
 22.273 50.230 -82 -95.077      3      4
     10 45.834  -1   -0.02    5.5   18.2
 82.439  0.133 100      64 46.204  30812
    551    1.2 1.1  94.022  6.818     77
  8.608  10010   3   50.94  100.2 0.3333
1 1
2 2

50.230 -82
45.834 -1

-10.181 15.910   0  78.309    192 59.743
 22.273 50.230 -82 -95.077      3      4
     10 45.834  -1   -0.02    5.5   18.2
 82.439  0.133 100      64 46.204  30812
    551    1.2 1.1  94.022  6.818     77
  8.608  10010   3   50.94  100.2 0.3333
2 1
4 3

-82 -95.077 3 4
-1 -0.02 5.5 18.2
100 64 46.204 30812

-10.181 15.910   0  78.309    192 59.743
 22.273 50.230 -82 -95.077      3      4
     10 45.834  -1   -0.02    5.5   18.2
 82.439  0.133 100      64 46.204  30812
    551    1.2 1.1  94.022  6.818     77
  8.608  10010   3   50.94  100.2 0.3333
4 5
1 1

100.2

Задача 4

City Bloxx е известна мобилна игра за строене на сгради. В нейния "Build city" режим, целта е построените сгради да се подредят в матрица 5 на 5.

Нека да разгледаме следните правила за сгради (в самата игра има някои разлики):

1. Жилищните сгради може да се поставят навсякъде.
2. Търговските сгради трябва да бъдат поставени до поне една жилищна сграда.
3. Офис сградите трябва да бъдат поставени до поне една жилищна и една търговска.
4. Луксозните сгради трябва да бъдат поставени до поне една жилищна, една търговска и една офис сграда.

Сгради са съседни само по вертикал и хоризонтал, не по диагонал.

От входа получавате масив 5 на 5 с цели числа, където с 1 до 4 се обозначават сградите, от жилищни до луксозни. Изкарайте дали подредбата на сградите е позволена (следва горните правила).

1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1

1 2 1 1 1
1 2 1 2 1
2 1 2 1 2
2 2 1 2 2
2 1 2 1 1

1 2 1 1 1
1 2 1 2 1
2 3 2 1 2
3 2 1 2 2
2 1 2 1 1

1 2 1 1 1
1 2 1 2 1
2 3 4 1 2
3 4 1 2 2
1 2 2 1 1

1 2 1 1 1
1 1 2 2 1
2 3 4 1 2
3 4 1 3 2
1 2 2 1 1

Задача 5

От входа получавате матрица 3 на 3, съствена от цели числа. Трябва да я транспонирате: да смените елементите над и под главния диагонал, и да изкарате резултата.

1 2 3
4 5 6
7 8 9

1 4 7
2 5 8
3 6 9

 8 13 0
-4  1 2
 0  0 5

 8 -4 0
13  1 0
 0  2 5

Задача 6

Напишете функция, която приема матрица с произволни размери, съствена от реални числа, заедно с два индекса. Разменете колоните на подадените индекси, ако това е възможно.

От входа получавате матрица 3 на 5, съствена от реални числа. След това получавате два индекса на колони.

Трябва да размените двете колони, използвайки вашата функция, и да изкарате резултата.

Вашия изход не е нужно да бъде подравнен.

 -16.01 -60.69    51   7.64 18.33
-100.41  22.16 17.07      9 30.07
  16.84  53.84 23.22 -21.11 0
0 3

  7.64 -60.69    51  -16.01 18.33
     9  22.16 17.07 -100.41 30.07
-21.11  53.84 23.22   16.84 0

 -16.01 -60.69    51   7.64 18.33
-100.41  22.16 17.07      9 30.07
  16.84  53.84 23.22 -21.11 0
0 0

 -16.01 -60.69    51   7.64 18.33
-100.41  22.16 17.07      9 30.07
  16.84  53.84 23.22 -21.11 0

 -16.01 -60.69    51   7.64 18.33
-100.41  22.16 17.07      9 30.07
  16.84  53.84 23.22 -21.11 0
4 2

 -16.01 -60.69 18.33   7.64    51
-100.41  22.16 30.07      9 17.07
  16.84  53.84 0     -21.11 23.22

Задача 7

От входа получавате матрица от букви 3 на 3. Тя определя шаблон, където буквата * означава, че всяка стойност е позволена.

След това от входа получавате матрица 6 на 6, съствена от букви. Трябва да намерите всички срещания на шаблона в тази матрица, като срещанията може да се застъпват!

1 2 3
4 5 6
7 8 9
1 2 3 1 2 3
4 5 6 4 5 6
7 8 9 7 8 9
1 2 3 1 2 3
4 5 6 4 5 6
7 8 9 7 8 9

= = =
. . .
= = =
= = = = = =
= = = = = =
. . . . . .
= = = = = =
. . . . . .
= = = = = =

1 2 3
4 * 5
6 7 8
1 2 3 1 2 3
4 a 5 4 b 5
6 7 8 6 7 8
1 2 3 1 2 3
4 c 5 4 d 5
6 7 8 6 7 8

* * *
* * *
* * *
1 2 3 1 2 3
4 5 6 4 5 6
7 8 9 7 8 9
1 2 3 1 2 3
4 5 6 4 5 6
7 8 9 7 8 9

Задача 8

От входа получавате две матрици 3 на 3, съствени от цели неотрицателни числа. Пресметнете умножението на матриците (ред по стълб) и изкарайте резултата.

2 1 3
3 4 1
5 2 3
1 2 0
4 1 2
3 2 1

15 11 5
22 12 9
22 18 7

2 1 3
3 4 1
5 2 3
1 2 0
4 1 2
3 2 1

8 9 5
21 12 19
17 13 14

Задача 9

При изграждането на устройства като клавиатури, често се използва "бутонна матрица". Няма да навлизаме в електрониката, но идеята е че когато натиснеш бутон, съответната колона и ред са "свързани"/активни.

Тоест, когато активни ред и колона се пресичат, тогава съответния бутон е натиснат.

Това означава, че се нуждаем да погледнем само състоянията на всеки ред и колона, и ще знаем всички натиснати бутони (вместо да поглеждаме всеки бутон поотделно).

Нека да разглеждаме стандартна 4 на 3 телефонна клавиатура[1]:

От входа първо получавате 4 булеви стойности: дали реда е активен (отгоре надолу). След това получавате още 3 булеви стойности: дали колоната е активна (отляво надясно).

Изкарайте кои бутони са натиснати, използвайки цифровите знаци, звезда (*) и диез (#). Ако няма натиснати, изкарайте съответно съобщение.

Задача 10

Триъгълника на Паскал е изчисление, при което се конструира триъгълник от числа. По двете "рамене" има единици, и всяко вътрешно число е сумата на горните две.

Пояснителна анимация[2]:

Генерирайте и изкарайте триъгълника на паскал в матрица 11 на 11, където двете страни на триъгълника са първата колона и главния диагонал.

Нека стойностите извън триъгълника да са нули.

Изход: (не е нужно да бъде подравнен)

1  0  0   0   0   0   0   0  0  0  0
1  1  0   0   0   0   0   0  0  0  0
1  2  1   0   0   0   0   0  0  0  0
1  3  3   1   0   0   0   0  0  0  0
1  4  6   4   1   0   0   0  0  0  0
1  5 10  10   5   1   0   0  0  0  0
1  6 15  20  15   6   1   0  0  0  0
1  7 21  35  35  21   7   1  0  0  0
1  8 28  56  70  56  28   8  1  0  0
1  9 36  84 126 126  84  36  9  1  0
1 10 45 120 210 252 210 120 45 10  1

Задача 11

От входа получавате матрица 10 на 10 от цели неотрицателни числа. След това получавате размер между 0 и 10.

Трябва да имплементирате "размазване", където всяка нова стойност на една клетка е равна на средната стойност на всички съседни клетки в "радиус" от подадения размер.

Тоест, ако размера е 2, тогава се взема средно аритметично на всяка клетка, която е на максимум две позиции разтояние, вертикално, хоризонтално и диагонално.

Ако размера е 0, тогава всяка клетка е средно аритметично на "себе си", т.е. не се променя. Не добавяйте към средното аритметично несъществуващи клетки (напр. клетката в горния ляв ъгъл няма клетки над или в ляво от себе си).

(Вашия изход не е нужно да бъде подравнен.)

0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 9 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 5 0 0 0 0 0
0 0 0 0 6 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 3 0 0 0 0 0 0 4 0
0 0 0 0 0 0 2 0 0 0
1

0.25  0.167 0.167 0     0     0     0     0     0     0
0.167 0.111 0.111 0     0     0     1     1     1     0
0.167 0.111 0.111 0     0     0     1     1     1     0
0     0     0     0.556 0.556 0.556 1     1     1     0
0     0     0     1.222 1.222 1.222 0     0     0     0
0     0     0     1.222 1.222 1.222 0     0     0     0
0     0     0     0.667 0.667 0.667 0     0     0     0
0.5   0.333 0.333 0     0     0     0     0.444 0.444 0.667
0.5   0.333 0.333 0     0     0.222 0.222 0.667 0.444 0.667
0.75  0.5   0.5   0     0     0.333 0.333 1     0.667 1.000

Задача 12

От входа получавате два реални координата, между (0,0) и (10,10).

Трябва да върнете матрица 10 на 10 от знаци, която се съставя единствено от шпации (spaces) и хиксове (x). Зачитаме, че координатите директно съответстват на матрицата, като (0,0) се намира в горния ляв ъгъл и (10,10) в долния десен.

В тази матрица, по подразбиране стоят само шпации. Хиксовете се намират там, където начертаната отсечка между входните точки би застъпила матрицата. Примерна диаграма:

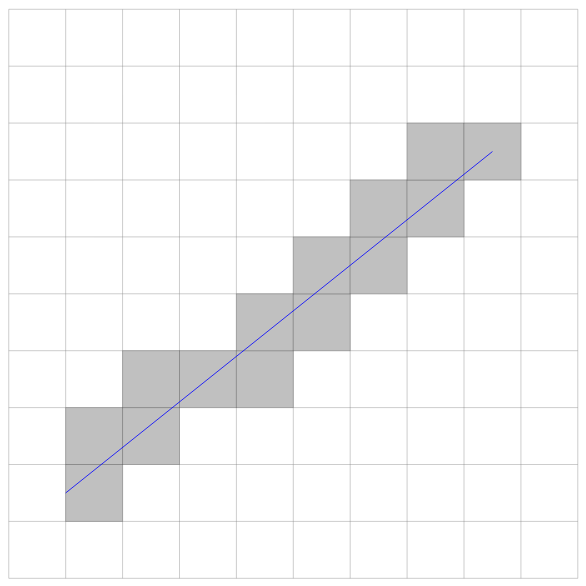
Тази операция се нарича интерполация.

Да се има впредвид, че спрямо използваната прецизност, някои стойности може да са шпации, когато трябва да са хиксове. Сравнявайте дали повечето стойности са коректни.

          
          
       xx 
      xx  
     xx   
    xx    
  xxx     
 xx       
 x        
          

За самоподготовка

Задача 13

От входа получавате матрица 8 на 8, съставена от символите точка и плюс. Трябва да върнете височината и ширината на най-големия правоъгълник, който застъпва всички плюсове.

. . . . . . . .
. . . . . . . .
. + + . + . . .
. . + . . . . .
. . + . . . + .
. . . . . . + .
. . + . . . . .
. . . . . . . .

. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .

+ . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . +

Задача 14

От входа приемате масив от 6 елемента и матрица с 6 реда и 3 колони, всички съставени от реални числа. Трябва да реализирате умножение на вектор по матрица (където масива е вектора).

1 2 3 4 5 6
1  7 13
2  8 14
3  9 15
4 10 16
5 11 17
6 12 18

1 2 1 0 2 1
3  1  8.8
0  1  2
5  1 15
5  1  0.1
0  1  7
0  1  0

Задача 15

От входа получавате матрица 9 на 7 с реални числа. След това получавате още едно реално число: максимална разлика.

Проверете дали данните са гладки: стойността във всяка една клетка да се различава с най-много максималната разлика от всички свои съседни клетки (по хоризонтала, вертикала и диагонала).

1 2 3 4 5 6 7
2 2 3 4 5 6 7
3 3 3 4 5 6 7
4 4 4 4 5 6 7
5 5 5 5 5 6 7
6 6 6 6 6 6 7
7 7 7 7 7 7 7
8 8 8 8 8 8 8
9 9 9 9 9 9 9
2

0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0.1

1 0 0 0 1 0 0
0 1 0 1 0 1 0
0 0 1 0 0 0 1
0 1 0 1 0 0 0
1 0 0 0 1 0 0
0 1 0 0 0 1 0
0 0 1 0 0 0 1
0 0 0 1 0 1 0
0 0 0 0 1 0 0
0.5

1 3 0 0 0 0 0
0 5 0 0 0 0 0
6 0 4 0 0 0 0
0 1 4 2 0 0 0
1 0 1 0 0 0 0
0 1 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 8 0 0
0 0 0 0 0 0 0
2

Задача 16

Напишете функция която приема матрица с произволни размери и "връща" матрица, която е като входната матрица, но всички елементи са "завъртяни" на дясно с 90 градуса.

Тоест, горния ляв елемент става горния десен, горния десен става долния десен и так. нат.

Не забравяйте да проверите дали можете да попълните завъртяната матрица в тазия която "връщате". Ако не можете, не записвайте нищо във върнатата.

От входа получавате матрица 4 на 8, съставена от цели числа. Използвайки вашата функция, завъртете матрицата и изкарайте резултата.

 1  2  3  4  5  6  7  8
 9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32

25 17  9 1
26 18 10 2
27 19 11 3
28 20 12 4
29 21 13 5
30 22 14 6
31 23 15 7
32 24 16 8

Задача 17

Трябва да реализирате (опростен вариант на) "pixel binning": спрямо подаден коефициент, стойностите в клетки се смесват.

Тоест, ако имаме binning от 2, тогава ще пресметнем средната стойност за всеки квадрат 2 на 2 и ще заменим всяка стойност от квадрата със средната.

От входа получавате матрица 12 на 12 с цели неотрицателни числа и неотрицателен binning коефициент. Трябва да върнете матрицата след приложен binning.

0 0 0 0 7 7 7 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 20 0 0
0 5 0 0 0 0 0 0 0 0 9 9
0 0 7 0 0 0 3 0 0 0 9 9
0 0 0 0 0 3 4 3 0 0 0 8
0 0 0 0 0 3 4 3 0 0 0 0
0 0 0 0 0 0 3 0 0 0 0 0
0 0 0 0 0 0 0 0 0 5 0 0
2 2 0 0 0 0 0 0 0 0 0 0
2 2 0 0 0 0 0 0 0 0 10 13
2 2 0 0 0 0 0 0 0 0 11 14
2

0.25 0.25 0    0    3.5  3.5  1.75 1.75 0    0    0   0
0.25 0.25 0    0    3.5  3.5  1.75 1.75 0    0    0   0
1.5  1.5  0    0    0    0    0    0    5    5    4.5 4.5
1.5  1.5  0    0    0    0    0    0    5    5    4.5 4.5
0    0    1.75 1.75 0.75 0.75 2.5  2.5  0    0    6.5 6.5
0    0    1.75 1.75 0.75 0.75 2.5  2.5  0    0    6.5 6.5
0    0    0    0    0.75 0.75 2.5  2.5  0    0    0   0
0    0    0    0    0.75 0.75 2.5  2.5  0    0    0   0
1    1    0    0    0    0    0    0    1.25 1.25 0   0
1    1    0    0    0    0    0    0    1.25 1.25 0   0
2    2    0    0    0    0    0    0    0    0    12  12
2    2    0    0    0    0    0    0    0    0    12  12

Задача 18

От входа получавате матрица 10 на 10 с цели неотрицателни числа. Трябва да върнете най-голямата подматрица, съставена само от единици.

Сравнявайте матриците по техния размер, тоест броя елементи. Ако има няколко еднакво големи подматрици, може да изкарате която и да е от тях.

0 0 0 0 0 0 1 1 1 1
0 0 0 0 0 0 1 1 1 1
0 0 0 0 0 0 1 2 1 1
0 1 1 1 0 0 1 1 1 1
0 1 1 1 0 0 1 1 1 1
0 1 1 1 0 0 0 0 0 0
0 1 1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 2 3 4 5
0 0 0 0 0 0 6 7 8 9

1 1 1
1 1 1
1 1 1
1 1 1

Задача 19

От входа получавате матрица 8 на 8 от реални числа. Реализирайте нещо, което ще наречем "сгъване" на матрицата, докато не остане само едно число.

Дефинираме сгъването така:

• сумираме горната половина на матрицата в долната половина, след това
• в долната половина, сумираме дясната половина в лявата (дясната една четвърт в лявата), след това
• в долната лява една четвърт, сумираме долната половина в горната,
• и така нататък

Накрая изкарате резултатното число.

1 2 3 4 5 6 7 8
9 1 2 3 4 5 6 7
8 9 1 2 3 4 5 6
7 8 9 1 2 3 4 5
6 7 8 9 1 2 3 4
5 6 7 8 9 1 2 3
4 5 6 7 8 9 1 2
3 4 5 6 7 8 9 0

Задача 20

Генерирайте и изкарайте триъгълника на Бел в долния ляв ъгъл на матрица 11 на 11. Това означава, че страните на триъгълника включват първата колона и главния диагонал.

• Започва се с единица.
• На всеки следващ ред, първия елемент е последния (ненулев) елемент на предходния ред.
• Всеки следващ елемент е сумата на предходния елемент в текущия ред и предходния елемент в горния ред.
• Спираме да сумираме, докато един от предходните ни елементи не бъде 0 (т.е. ако ще сумираме нещо с 0).

Пояснителна анимация[3]:

Тази задача е подобна на Задача 10.

Изход: (не е нужно да бъде подравнен)

     1      0      0      0      0      0      0      0      0      0      0
     1      2      0      0      0      0      0      0      0      0      0
     2      3      5      0      0      0      0      0      0      0      0
     5      7     10     15      0      0      0      0      0      0      0
    15     20     27     37     52      0      0      0      0      0      0
    52     67     87    114    151    203      0      0      0      0      0
   203    255    322    409    523    674    877      0      0      0      0
   877   1080   1335   1657   2066   2589   3263   4140      0      0      0
  4140   5017   6097   7432   9089  11155  13744  17007  21147      0      0
 21147  25287  30304  36401  43833  52922  64077  77821  94828 115975      0
115975 137122 162409 192713 229114 272947 325869 389946 467767 562595 678570

Задача 21

От входа получавате матрица 3 на 4 от реални числа и след това височина и дължина на изходната матрица.

Трябва да "реоразмерите" матрицата, като запазите последователността на елементи отляво надясно, отгоре надолу. Височината и дължаната няма да са повече от 10.

Ако изходната матрица е по-голяма, попълнете празните позиции с нули.

1  2  3  4
5  6  7  8
9 10 11 12
4 5

 1  2 3 4  5
 6  7 8 9 10
11 12 0 0  0
 0  0 0 0  0

1  2  3  4
5  6  7  8
9 10 11 12
4 2

1 2
3 4
5 6
7 8

Задача 22

От входа получавате матрица 3 на 3 със знаци. След това получавате число "режим", което е 1, 2 или 3.

Трябва да изкарате матрица със знаци 9 на 9, в която е попълнено изображението спрямо режима.

1. Режим 1 обозначава повтаряне, където изображението се повтаря последователно
2. Режим 2 обозначава "border", където изображението се слага в центъра и останалта част се попълва със знак диес #.
3. Режим 3 обозначава "clamp", изображението се слага в центъра и останалата част се попълва като се повтаря последната буква. Тоест, дясното 3 на 3 се попълва с повторение на десния знак.

a b c
d * e
f g h
1

a b c a b c a b c
d * e d * e d * e
f g h f g h f g h
a b c a b c a b c
d * e d * e d * e
f g h f g h f g h
a b c a b c a b c
d * e d * e d * e
f g h f g h f g h

a b c
d * e
f g h
2

# # # # # # # # #
# # # # # # # # #
# # # # # # # # #
# # # a b c # # #
# # # d * e # # #
# # # f g h # # #
# # # # # # # # #
# # # # # # # # #
# # # # # # # # #

a b c
d * e
f g h
3

a a a b b b c c c
a a a b b b c c c
a a a b b b c c c
d d d a b c e e e
d d d d * e e e e
d d d f g h e e e
f f f g g g h h h
f f f g g g h h h
f f f g g g h h h

Задача 23

От входа получавате цяло неотрицателно число, по-малко от 50. Трябва да изкарате спирала от това число към нула (включително), която се движи от началното число до нула обратно на часовниковата стрелка, като 1цата е в дясно от нулата.

Зачитайте, че 0 винаги е в центъра на спиралата и се въртите първо с една позиция разстояние, после с две и так. нат.

(Вашия изход не е нужно да бъде подравнен.)

  0 1
4 3 2

5 0 1
4 3 2

6 7 8 9
5 0 1 10
4 3 2

 6  7  8  9
 5  0  1 10
 4  3  2 11
15 14 13 12

За любознателни

Задача 24

Реализирайте матричен калкулатор. От входа получавате матрица 4 на 4 с реални числа и след това получавате редица операции.

Всяка операция започва с буква, като буквата $ сигнализира край на програмата. След всеки знак има няколко аргумента, т.е. допълнителни стойности които трябва да се въведат, преди операцията да се изпълни.

• Операцията * обозначава умножение на ред, и след знака има цяло неотрицателно число за индекс на ред и след него е реално число (коефициент с който да умножим реда).
• Операцията + обозначава сума на редове, след знака се очакват два неотрицателни индекса на редове, първия ред се сумира в втория
• Операцията ^ обозначава размяна на редове, след знака се очакват два неотрицателни индекса на редове и стойностите им се разменят.

След всяка операция (освен $) трябва да изкарате състоянието на матрицата.

Задача 25

Трябва да реализирате Играта "Живот".

От входа получавате матрица 10 на 10 с булеви стойности. След това получавате неотрицателно число: брой генерации (ходове).

Всяка клетка наричаме жива или мъртва (съответно на true или false). В една генерация (ход) на играта, всяка клетка променя своя статус (стойност) по следните правила:

• всяка жива клетка с по-малко от два живи съседа (вертикално, хоризонтално и диагонално) умира
• всяка жива клетка с два или три живи съседа остава жива
• всяка жива клетка с повече от три живи съседа умира
• всяка мъртва клетка с точно три живи съседа оживява