Задачи - УПП, Седмица 6, 06.11.2025
GitHub Classroom: https://classroom.github.com/a/JSB1UK_f
За решаване
Задача 1
През 1837 година, Чарлз Бабидж пита въпроса:
What is the smallest positive integer whose square ends in the digits 269,696?
Според него това число е 99736 (чиито квадрат е 9947269696). Напишете програма, която намира най-малкото число, отговарящо на въпроса.
| Вход | Изход |
|---|---|
| 25264 |
Задача 2
От входа получавате 8 цели положителни числа. Трябва да изкарате най-голямото общо делимо между всички тези числа.
| Вход | Изход |
|---|---|
| 8 8 8 8 8 8 8 8 | 8 |
| 2 6 14 8 20 4 12 14 | 2 |
| 318 577 200 235 72 333 947 37 | 1 |
Задача 3
Получавате цяло положително число. В него трябва да замените всички срещания на най-срещаната цифра с 0.
Ако има няколко такива цифри, трябва да замените само най голямата от тях.
| Вход | Изход |
|---|---|
| 1 | 0 |
| 5 | 0 |
| 10 | 0 |
| 15 | 10 |
| 99 | 0 |
| 9988 | 88 |
| 138783 | 130703 |
| 535735737 | 535035030 |
Задача 4
Получавате една редица от 15 цели числа и след това втора редица с 5 цели уникални числа. Трябва да върнете броя срещания в първата редица на всяко от числата във втората редица.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 | 1 1 1 1 1 |
| 1 2 2 1 1 2 0 2 1 1 0 2 2 1 1 -9 0 1 2 300 | 0 2 7 6 0 |
Задача 5
От входа получавате две реални числа: координати на точка в равнината. Спрямо следното изображение:
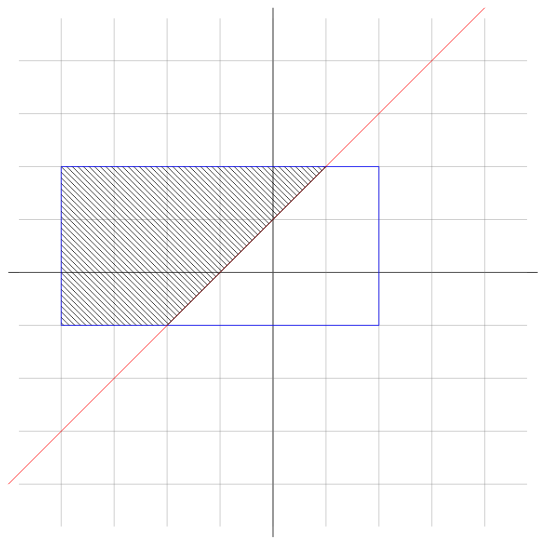
изкарайте дали точката е в защрихованата област или не. Областта не включва правата и правоъгълника!
Зачитайте, че черните прави отбелязват главните оси, а разстоянията между съседни сиви оси е единица.
| Вход | Изход |
|---|---|
| 0 0 | Outside |
| -1 0 | Outside |
| -1.1 0 | Inside |
| -2 1 | Inside |
| -4 2 | Outside |
| -3.9 1.9 | Inside |
| -4 -1 | Outside |
| -3.9 -0.9 | Inside |
| 1 2 | Outside |
| 0.9 2 | Outside |
| 1 1.9 | Outside |
| 0.9 1.9 | Outside |
| 0.8 1.9 | Inside |
Задача 6
От входа получавате цяло положително число. Трябва да върнете дали то е щастливо.
Нека да вземем нашето число и да го заменим със сумата на всички свои цифри, повдигнати на квадрат. Оригиналното число е щастливо, ако след краен брой прилагания на тази операция, получим числото 1.
Когато число не е щастливо, влизаме в безкрайния цикъл 4, 16, 37, 58, 89, 145, 42, 20, 4, 16, ... Това е единствения възможен цикъл в който нещастно число може да попадне.
| Вход | Изход |
|---|---|
| 1 | Happy |
| 7 | Happy |
| 14 | Not happy |
| 28 | Happy |
| 318 | Not happy |
| 319 | Happy |
| 320 | Happy |
| 888 | Happy |
Задача 7
От входа получавате 6 реални числа. Пресметнете съответните 6 префиксни суми и ги изкарайте.
Това са сумите на всички числа до сега. Тоест, префиксната сума на второто число е сумата на първото и второто число. Префиксата сума на третото число е сумата на първото, второто и третото число.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 | 1 3 6 10 15 21 |
| 30.86 967.214 85 515.27 -453 -37.79 | 30.86 998.074 1083.07 1598.34 1145.34 1107.55 |
Задача 8
От входа получавате две реални числа: координати на точка в равнината. Спрямо следното изображение:
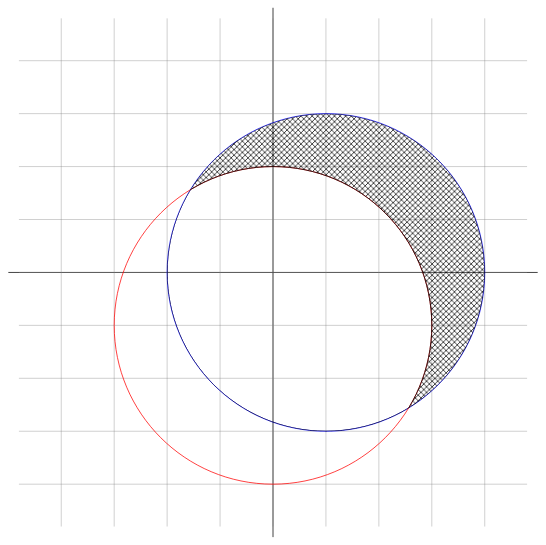
изкарайте дали точката е в защрихованата област или не. Областта не включва самите окръжности!
Зачитайте, че черните прави отбелязват главните оси, а разстоянията между съседни сиви оси е единица.
| Вход | Изход |
|---|---|
| 1 1 | Outside |
| -1.5 -2.5 | Outside |
| 0 2 | Outside |
| 0 2.1 | Inside |
| -1 2 | Inside |
| 4 0 | Outside |
| 3.9 0 | Inside |
| 3 0 | Inside |
| 3 -1 | Outside |
| 3 -2 | Inside |
| 2.586 -2.5356 | Inside |
| 2.5356 -2.586 | Outside |
| -1.54 1.584 | Inside |
| -1.55 1.55 | Outside |
Задача 9
От входа получавате 10 цели числа. Трябва да върнете дали сред тях същестуват три числа (на различни позиции), чиято сума е равна на 0.
| Вход | Изход |
|---|---|
| 1 -2 3 -4 5 -6 7 -8 9 -10 | Exists |
| 2 4 45 6 -10 5 -45 8 23 11 | Exists |
| 1 4 45 6 -11 4 -45 8 23 11 | Doesn't exist |
Задача 10
От входа получавате четири трицифрени цели неотрицателн числа. Трябва да върнете най-голямото възможно цяло число, което се получава след "слепване" на тези числа.
Не е нужно да използвате сортиращ алгоритъм!
| Вход | Изход |
|---|---|
| 100 200 300 400 | 400300200100 |
| 552 285 732 937 | 937732552285 |
| 492 352 289 382 | 492382352289 |
Задача 11
От входа получавате две реални числа: координати на точка в равнината. Спрямо следното изображение:
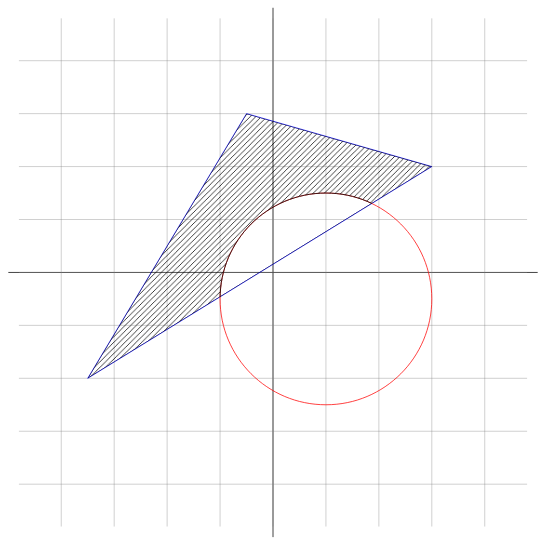
Областта не включва правата и правоъгълника!
Зачитайте, че черните прави отбелязват главните оси, а разстоянията между съседни сиви оси е единица.
| Вход | Изход |
|---|---|
| -1 1 | Inside |
| -1 -1 | Outside |
| -2 -1 | Inside |
| 2 2 | Inside |
| 3 2 | Outside |
| 2.9 2 | Inside |
| 0 1.5 | Inside |
| 1 1.5 | Outside |
| 2 1.5 | Inside |
| 2 1.1 | Outside |
| -3.354 -1.831 | Inside |
| 1.864 1.356 | Inside |
| 1.73 1.287 | Outside |
За самоподготовка
Задача 12
От входа получавате цяло неотрицателно число. Трябва да върнете дали е число на "сума-произведение".
С други думи, дали е равно на сумата на цифрите си, умножено по умнежнието на цифрите.
| Вход | Изход |
|---|---|
| 0 | Sum-product number |
| 2 | Not a sum-product number |
| 22 | Not a sum-product number |
| 135 | Sum-product number |
| 1337 | Not a sum-product number |
Задача 13
От входа получавате цяло положително число. Трябва да върнете всички негови делители.
| Вход | Изход |
|---|---|
| 5 | 1 5 |
| 15 | 1 3 5 |
| 16 | 1 2 4 8 16 |
| 137 | 1 137 |
| 864 | 1 2 3 4 6 8 9 12 16 18 24 27 32 36 48 54 72 96 108 144 216 288 432 864 |
Задача 14
От входа получавате две цели неотрицателни числа. Трябва да намерите тетрацията на първото числото на степен второто число.
Както нормалното степенуване е повторено умножение, така тетрацията е повторено степенуване. Число на тетрация "степен" озачава, че числото се повдига на нормална степен себе си, тетрация степен на брой пъти.
Тетрацията расте бързо, използвайте най-големия възможен тип.
| Вход | Изход |
|---|---|
| 2 4 | 65536 |
| 3 1 | 3 |
| 3 2 | 27 |
| 3 3 | 7625597484987 |
| 8 2 | 16777216 |
Задача 15
От входа получавате 8 цели неотрицателни числа. Трябва да върнете най-малкото общо кратно на всеки две съседни числа.
Най-малко общо кратно е най-малкото число, което се дели без остатък на двете числа.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 | 2 6 12 20 30 42 56 |
| 4 6 9 389 13 13 2 8 | 12 18 3501 5057 13 26 8 |
Задача 16
От входа получавате две реални числа: координати на точка в равнината. Спрямо следното изображение:
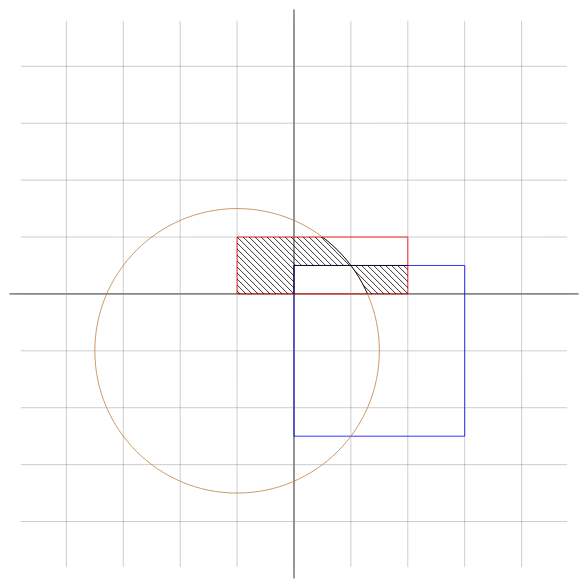
изкарайте дали точката е в защрихованата област или не.
Зачитайте, че всяка сива права отбелязва брой единици разстояние от нулата.
| Вход | Изход |
|---|---|
| 0 0 | Outside |
| -1 -1 | Outside |
| -0.5 -0.5 | Inside |
| 0 0.75 | Inside |
| 2 0 | Outside |
| 1.5 0 | Outside |
| 1.5 0.1 | Inside |
| 1 0.5 | Outside |
Задача 17
От входа получавате две естествени числа, a и b.
Трябва да върнете дали a е унитарен делител на b.
Това е изпълнено, когато a е делител на b и най-големия общ делител на a и b / a е 1.
| Вход | Изход |
|---|---|
| 5 60 | Unitary divisor |
| 6 60 | Not a unitary divisor |
| 5 10 | Unitary divisor |
| 4 12 | Unitary divisor |
| 6 12 | Not a unitary divisor |
Задача 18
От входа получавате 10 реални числа. Трябва да върнете най-голямата възможна сума, получена чрез събиране на колкото и дълга последователна редица от елементи.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 9 10 | 55 |
| -2 -1 0 1 2 3 4 5 6 7 | 28 |
| -2 1 -3 4 -1 2 1 -5 4 -9 | 6 |
| -4 13.3 5.5 7 -6.5 10 0 -15 2.1 3 | 29.3 |