Задачи - УПП, Седмица 5, 30.10.2025
GitHub Classroom: https://classroom.github.com/a/6oPRMxJx
Имайте предвид, че не всички задачи се решават с масиви!
За решаване
Задача 1
От входа получавате 10 реални числа. Трябва да ги върнете в обратен ред.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 9 10 | 10 9 8 7 6 5 4 3 2 1 |
| 41.4 89.95 65 34.799 18.62 100.001 84.55 69.21 6 39.8 | 39.8 6 69.21 84.55 100.001 18.62 34.799 65 89.95 41.4 |
Задача 2
От входа получавате 7 букви. Трябва да изкарате буквите в същата последователност, обаче завъртяни надясно с 3 позиции.
| Вход | Изход |
|---|---|
| a b c d e f g | e f g a b c d |
| k l m l j l b | j l b k l m l |
Задача 3
От входа получавате 14 цели неотрицателни числа. Трябва да изкарате второто най-голямо число. Ако няма такова, просто изкарайте най-голямото.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 | 13 |
| 505 19 899 0 232 61 546 6 65 259 55 389 326 760 | 760 |
| 9 9 9 9 9 9 9 9 9 9 9 9 9 9 | 9 |
Задача 4
От входа получавате две цели положителни числа. Трябва да върнете факториел от първото число, който факториел е повдигнат на степен второто число.
Факториел на едно (неотрицателно цяло) число е умножението на всички цели числа от 1 до самото число включително.
Примерно, факториел от 5 е 1 * 2 * 3 * 4 * 5 = 120.
| Вход | Изход |
|---|---|
| 5 1 | 120 |
| 5 2 | 14400 |
| 3 6 | 46656 |
| 4 3 | 13824 |
| 1 183 | 1 |
| 2 8 | 256 |
Задача 5
От входа получавате 18 цели числа. Трябва да изкарате същата поредица числа, обаче всички нули са в началото на редицата.
| Вход | Изход |
|---|---|
| 1 0 0 2 3 4 0 5 0 6 0 0 0 7 8 0 9 0 | 0 0 0 0 0 0 0 0 0 1 2 3 4 5 6 7 8 9 |
| 0 839 643 42 -694 57 650 729 -434 0 35 155 176 873 40 0 658 0 | 0 0 0 0 839 643 42 -694 57 650 729 -434 35 155 176 873 40 658 |
Нужни ли са масиви, ако в условието трябваше да изкарвате нулите в края на поредицата?
Задача 6
От входа получавате 15 цели числа. Трябва да изкарате дължината на най-дългата последователност от числа, която е подредена в нарастващ ред.
Последователност от числа, която съдържа еднакви числа, също се зачита за сортирана в нарастващ ред.
| Вход | Изход |
|---|---|
| 1 2 3 0 0 0 6 7 8 8 8 -3 -2 -1 0 | 8 |
| 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 | 15 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | 15 |
| 4 -4 4 -4 4 -4 4 -4 4 -4 4 -4 4 -4 4 | 2 |
| 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 | 1 |
| -539 -118 -431 53 -151 -151 -82 -40 640 -47 347 -50 -100 -198 984 | 5 |
Задача 7
От входата получавате цяло неотрицателно число. Върнете дали то е перфектно: дали е равно на сумата на всички свои делители, освен себе си.
| Вход | Изход |
|---|---|
| 6 | Perfect |
| 7 | Not perfect |
| 1337 | Not perfect |
| 27 | Not perfect |
| 28 | Perfect |
| 29 | Not perfect |
| 33550336 | Perfect |
| 496 | Perfect |
| 42 | Not perfect |
| 8128 | Perfect |
Задача 8
От входа получавате две редици от по 10 реални числа (т.е. първите 10 числа са от първата редица, и вторите 10 числа образуват втората редица).
След това получавате знак - аритметича операция (+, -, *, /).
Трябва да изпълните операцията върху всяка съответна двойка числа от двете редици и да върнете резултатите.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 + |
2 4 6 8 10 12 14 16 18 20 |
| 4.5 -16 194.1 919.01 1000.11 -27 12 444 71 0 0 8 12 56 10 0 3 14 1 0 / |
inf -2 16.175 16.41 100.011 -inf 4 31.714 71 -nan |
Задача 9
От входа получавате реално число z между 0 (изключително) и 2 (включително), заедно с дължина n.
Трябва да намерите стойността на логаритъм с основа ℯ (Неперово число) от това число, използвайки развитието по ред на Тейлър:
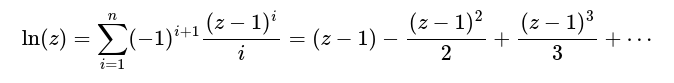
като n определя колко елемента от реда да използвате.
| Вход | Изход |
|---|---|
| 1 1 | 0 |
| 1.5 1 | 0.5 |
| 1.5 3 | 0.416667 |
| 1.5 9 | 0.405532 |
| 1.5 20 | 0.405465 |
| 0.5 1 | -0.5 |
| 0.5 5 | -0.688542 |
| 0.5 20 | -0.693147 |
| 0.01 20 | -3.40687 |
| 0.01 900 | -4.60516 |
| 0.01 1000 | -4.60517 |
Задача 10
От входа получавате цяло неотрицатено число с максимум 8 цифри. Това число представлява сериен номер под S10 стандарта за идентификационни номера на пратки.
Трябва да пресметнете "контролната цифра" (check digit) на серийния номер. Това става по следния начин:
- От ляво на дясно, трябва да умножите всяка цифра със съответната си "тежест": 8, 6, 4, 2, 3, 5, 9, 7
- Сумирате умножените цифри
- Пресмятате контролната цифра по формулата:
11 - <сума> mod 11, където ако резултата е 10, цифрата е 0 и ако резултата е 11, цифрата е 5.
| Вход | Изход |
|---|---|
| 0 | 5 |
| 1 | 4 |
| 2 | 8 |
| 8 | 0 |
| 47312482 | 9 |
| 87654321 | 6 |
| 37153644 | 4 |
| 30159181 | 5 |
Задача 11
От входа получавате цяло неотрицателно число.
Изкарвате числото на Лукас след толкова на брой позиции и ако числото не е било 0, приемаме ново число и повтаряте логиката.
Тоест, ако първото число е n, тогава връщате n-тото число на Лукас.
Ако второто число е m, тогава връщате n + m-тото число на Лукас.
И така нататък.
Числата на Лукас се определят по следния начин:
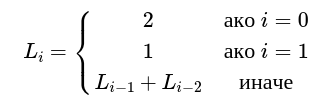
Вашия вход и изход може да са смесени!
| Вход | Изход |
|---|---|
| 0 | 2 |
| 1 0 | 1 1 |
| 2 0 | 3 3 |
| 5 0 | 11 11 |
| 2 3 0 | 3 11 11 |
| 8 8 1 0 | 47 2207 3571 3571 |
Задача 12
От входа получавате 20 цели числа, всяко от които е индекс на елемент в масива (т.е. всяко е между 0 и 19 включително).
Започвайки от първия елемент, вземате числената му стойност като индекс и "отивате" на тази позиция в масива. Аналогично, за текущия елемент, вземате числената стойност и индексирате. Така продължавате, докато не стигнете до последния елемент, когато алгоритъма спира.
Целта е да преброите колко пъти "скачате" между различни числа и да изкарате тази бройка.
Ако се поражда цикъл (посетим някое число повече от един път), тогава трябва да изкарате "Infinity".
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 0 | 19 |
| 19 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | 1 |
| 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 | Infinity |
| 5 3 18 19 12 2 7 14 17 16 19 13 11 6 9 19 3 1 8 1 | 8 |
| 4 3 18 9 12 2 7 14 17 16 19 13 11 6 9 19 3 1 8 1 | Infinity |
За самоподготовка
Задача 13
От входа получавате 8 цели числа. След това получавате 9то цяло число.
Трябва да върнете, сред 8те цели числа, колко често се среща 9тото.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 9 | 0 |
| 1 2 1 -3 2 -4 3 5 1 | 2 |
| 8 1 7 8 8 1 7 -3 8 | 3 |
| 0 0 0 0 0 0 0 0 0 | 8 |
Задача 14
От входа получавате 16 цели числа. Трябва да изкарате, на два реда, първо всички четни числа и после всички нечетни.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | 2 4 6 8 10 12 14 16 1 3 5 7 9 11 13 15 |
| -961 -46 86 871 657 96 -40 -297 -754 468 -5 662 -9 -392 82 255 | -46 86 96 -40 -754 468 662 -392 82 -961 871 657 -297 -5 -9 255 |
Задача 15
От входа получавате 12 реални числа. Трябва да върнете, на отделни редове, двойки числа от тази поредица:
- Първата двойка числа съдържа първото и последното число.
- Втората двойка има второто и пред-посленото число.
- И така нататък.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 9 10 11 12 | 1 12 2 11 3 10 4 9 5 8 6 7 |
| 419.8 124.01 -47 915.5 31.99 769.89 505 58 -568.5 547.77 899.192 52 | 419.8 52 124.01 899.192 -47 547.77 915.5 -568.5 31.99 58 769.89 505 |
Задача 16
От входа получавате две редици от по 5 цели числа (т.е. първите 5 числа са част от първата редица и вторите 5 числа са част от втората).
Трябва да изкарате една редица от числа, където двете редици са преплетени: първо имаме първото число от първата редица, след това първото число от втората редица, след това второто число от първата редица и така нататък.
| Вход | Изход |
|---|---|
| 1 2 3 4 5 6 7 8 9 10 | 1 6 2 7 3 8 4 9 5 10 |
| 0 1 0 1 0 1 0 1 0 1 | 0 1 1 0 0 1 1 0 0 1 |
Задача 17
От входа получавате цяло число в десетична бройна система.
Трябва да изкарате дали то е число на Армстронг: число, което е равно на сумата на цифрите си, където всяка цифра е повдигната на степен, дължината на числото.
| Вход | Изход |
|---|---|
| 153 | Narcissistic |
| 5 | Narcissistic |
| 0 | Narcissistic |
| 10 | Not narcissistic |
| 407 | Narcissistic |
| 54748 | Narcissistic |
Задача 18
От входа получавате 7 цели числа.
Трябва да намерите индекса на равновесие: позиция сред числата, такава че сумата от първото число до индекса - 1 е равна на сумата на числата от индекса + 1 до последното число.
Ако такаъв индекс не съществува, изкарате "No such index".
| Вход | Изход |
|---|---|
| -7 1 5 2 -4 3 0 | 3 |
| 5 5 4 2 1 3 8 | No such index |
Задача 19
От входа получавате две числа: реален ъгъл в радиани x и положителен максимален индекс n.
Трябва да върнете стойността на синус от този ъгъл, използвайки реда на Тейлър:
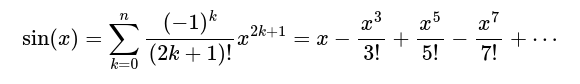
където n определя с колко елемента от реда да смятаме.
| Вход | Изход |
|---|---|
| 0 1 | 0 |
| 0.52359 15 | 0.499992 |
| 1.57079 15 | 0.998356 |
| 4.71238 5 | -1.08189 |
Задача 20
От входа получавате цяло положително число. Трябва да валидирате това число използвайки алгоритъма на Luhn:
- Най-дясната цифра е "цифра за проверка", тя трябва да бъде изкарана за после.
- Започвайки от най-дясната цифра (от останалите цифри, т.е. втората най-дясна в числото), трябва да умножите всяка втора цифра по две. Ако цифрата стане по-голяма от 9, трябва да извадите 9.
- Сумирате всички цифри (всички умножени и неумножени).
- Проверявате дали цифрата за проверка е равна на
(10 - (сумa mod 10)) mod 10
Този алгоритъм се използва главно в проверката на номера на дебитни/кредитни карти. Главната цел е да се засекат някои механични грешки при въвеждане на номера.
| Вход | Изход |
|---|---|
| 0 | Valid |
| 1 | Invalid |
| 1156 | Valid |
| 1337 | Invalid |
| 12345674 | Valid |
| 13245674 | Invalid |
Задача 21
От входа получавате цяло неотрицателно число. Трябва да върнете съответното по индекс число на Каталан.
n-тото число на Каталан се дефинира по следния начин:
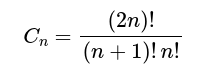
Където x! е факториел от x.
Припомняме, че факториел на едно число е умножението на всички цели числа от 1 до самото число включително.
| Вход | Изход |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 5 | 42 |
| 9 | 4862 |