Задачи - УПП, Седмица 3, 16.10.2025
GitHub Classroom: https://classroom.github.com/a/UMc2WhVX
За решаване
Задача 1
Получавате цяло число. Трябва да върнете 0 ако е нечетно и 1 ако е четно.
| Вход | Изход |
|---|---|
| 5 | 0 |
| 10 | 1 |
Задача 2
Получавате главна буква. Трябва да върнете съответната малка буква.
| Вход | Изход |
|---|---|
| A | a |
| Z | z |
| U | u |
Задача 3
Получавате 3 цели числа, трябва да върнете 1 ако образуват аритметична прогресия и 0 иначе.
| Вход | Изход |
|---|---|
| 1 2 3 | 1 |
| 4 5 7 | 0 |
| 4 6 7 | 0 |
| -3 5 13 | 1 |
Задача 4
Получавате цяло неотрицателно 32-битово число и "позиция", което е цяло неотрицателно число между 0 и 31.
Трябва да върнете бит-а на съответната позиция в числото, като индекс 0 е най-десния бит (младши), докато 31 е най-левия бит (старши).
| Вход | Изход |
|---|---|
| 5 0 | 1 |
| 5 1 | 0 |
| 5 2 | 1 |
| 4227842047 14 | 0 |
| 1073741824 30 | 1 |
Задача 5
Получавате десетично число: сума в левове.
Трябва да върнете същата сума в евро, като 1 € = 1.95583 лв.
Поради прецизност при такива числа, вашите изходи може с много малко да се различават.
| Вход | Изход |
|---|---|
| 1 | 0.511292 |
| 1.95583 | 1 |
| 15 | 7.66938 |
| 199.99 | 102.253 |
| 450 | 230.081 |
Задача 6
Получавате две булеви стойности. Трябва да върнете 1 ако свойството "би-импликация" е изпълнено за тях. Иначе върнете 0.
Припомняме, че би-импликацията и импликацията се дефинират по следния начин:
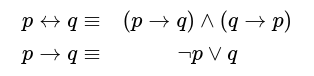
| Вход | Изход |
|---|---|
| 0 1 | 0 |
| 1 1 | 1 |
| 1 0 | 0 |
| 0 0 | 1 |
Задача 7
Получавате 4 цели числа от входа. За тях трябва да изкарате:
- средно аритметично,
- сума,
- сума от вида
1/<първо число> + 1/<второ число> + ..., - умножение.
| Вход | Изход |
|---|---|
| 1 2 3 4 | 2.5 10 2.08333 24 |
| 13 151 7 29 | 50.0 200 0.260886 398489 |
| -293 6 0 -1 | -72.0 -288 inf 0 |
Задача 8
Получавате 5 реални числа: коефициентите на полином от трета степен a (a различно от 0), b, c, d и потенциален негов корен x.
Трябва да върнете 1 ако x е корен на уравнението и 0 ако не е.
Припомняме, че x е корен на кубично уравнение, когато:
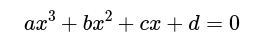
| Вход | Изход |
|---|---|
| 2 3 -11 -6 2 | 1 |
| 2 3 -11 -6 -0.5 | 1 |
| 2 3 -11 -6 -3 | 1 |
| 2 3 -11 -6 -2 | 0 |
| 3 -3 -90 0 0 | 1 |
| 5 -2 5 -2 0.4 | 1 |
Задача 9
Получавате цяло неотрицателно 8-битово число. Трябва да върнете 1 ако броя единици в числото е нечетно и 0 иначе.
| Вход | Изход |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 255 | 0 |
| 238 | 0 |
| 239 | 1 |
Задача 10
Получавате 6 реални числа: коефициентите на два (ортонормирани) триизмерни вектора. Върнете тяхното точково умножение.
Припомняме, че алгебричата дефиниция на точковото умножение е:
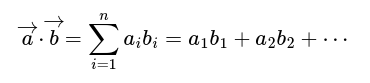
| Вход | Изход |
|---|---|
| 1 3 -5 4 -2 -1 | 3 |
| 1.5 2.45 3.8 1.01 5 7.005 | 40.384 |
| -1 -2 3 4 0 -8 | -28 |
| 3 2 1 6 5 2 | 30 |
Задача 11
Получавате две 32-битови цели неотрицателни числа. Всеки 8 бита в тях образуват подчисло.
Сумирайте съответните подчисла в двете числа и изкарайте резултаното "надчисло".
| Вход | Изход |
|---|---|
| 3 4 | 7 |
| 255 1 | 0 |
| 768 1024 | 1792 |
| 196608 262144 | 458752 |
| 50331648 67108864 | 117440512 |
| 4283629573 21629434 | 10291711 |
За самоподготовка
Задача 12
Първите релефни етикети (които човек може сам да попълни) са въведени през 1958 от DYMO.
Механични устройства съдържат диск с букви (знаци), който се завърта докато не се избере желаната буква. Чрез стискане на дръжката, малък чук прищипва лентата върху диска (който има релефи на буквите), пластмасовата лента се изкривява и буква се отпечтва (подобно на пишеща машина).
Нека нашия диск съдържа само малки букви. Във входа получавате две малки букви: коя буква е избрана в момента и коя буква е желана. Трябва да върнете с колко позиции на дясно (по часовниковата стрелка) трябва да се завърти диска, така че желаната буква да се избере.
| Вход | Изход |
|---|---|
| a a | 0 |
| a b | 1 |
| a z | 25 |
| z a | 1 |
| k j | 25 |
| w d | 7 |
Задача 13
През 629, индийския математик Бхаскара 1ви представя една забележителна апроксимация на синус функцията (в радиани):
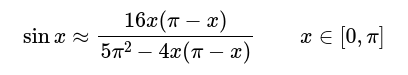
От входа ще получите два ъгъла (в радиани): α и β.
Използвайки единствено апроксимацията на Бхаскара 1ви, пресметнете tg(α + β).
За константата π, използвайте поне 5 цифри след десетичната запетая.
| Вход | Изход |
|---|---|
| 0 0 | 0 |
| 1.047196 1.047196 | 0.864865 |
| 0 0.785397 | 0.705882 |
| 1.570795 1.570795 | 0 |
| 0.785397 0.785397 | 1 |
| 1.570795 0.785397 | 0.705883 |
Задача 14
От 1970те, в компютрите един от най-често употребяваните методи за представяне на време е така нареченото "UNIX време". Това е 32-битово цяло число, обозначаващо изминалите секунди от 00:00:00 часа UTC на 1 Януари 1970 година.
Очевидни лимитации на тази схема са, че най-ранната възможна дата е в края на 1901 и най-късната в началото на 1938. След малко над 12 години, тази схема няма да може да представя текущата дата и час.
Получавате цяло 32 битово число. То представлява UNIX време. Трябва да изкарате UTC часа и датата, в "човешки" формат ("час:минути:секунди ден месец година").
| Вход | Изход |
|---|---|
| 0 | 0:0:0 1 1 1970 |
| −31536000 | 0:0:0 1 1 1969 |
| 1095379199 | 23:59:59 16 9 2004 |
| 2147483647 | 3:14:7 19 1 2038 |
| −2147483648 | 20:45:52 13 12 1901 |
| 1760252774 | 7:6:14 12 10 2025 |
Задача 15
В модерния интернет, всяко устройство се обозначава с уникален адрес. Това е 32-битово цяло неотрицателно число.
За човешко удобоство, това число се представя чрез "dot-decimal notation": всеки 8 бита се представят като десетично число и тези 4 числа се слепват с точки между тях.
Например, адресът 2130706433 е двоичното 01111111000000000000000000000001, което като се разбие на по 8 бита става 01111111, 00000000, 00000000 и 00000001, и всички те като се обединят с точки и се предствят в десетична бройна система, резултата е 127.0.0.1
От входа получавате цяло неотрицателно 32-битово число. Трябва да изкарате стойността му в "dot-decimal notation".
| Вход | Изход |
|---|---|
| 2130706433 | 127.0.0.1 |
| 3232235521 | 192.168.0.1 |
| 1043096983 | 62.44.101.151 |
| 3494943456 | 208.80.154.224 |
| 134744072 | 8.8.8.8 |
| 3625466119 | 216.24.57.7 |
Задача 16
Получавате 8 реални числа: всеки две последователни образуват координат в равнината. Първите два координата представят горния ляв и долния десен ъгъл на първи правоъгълник. Вторите два координата представят горния ляв и долния десен ъгъл на втори правоъгълник.
Трябва да върнете 1 ако правоъгълниците се пресичат и 0 иначе.
| Вход | Изход |
|---|---|
| 0 6 4 0 6 6 8 2 | 0 |
| 0 6 4 0 4 6 8 2 | 1 |
| 0 6 4 0 3 3 8 2 | 1 |
| -3 4.5 2.1 0.5 0 6 4 0 | 1 |
| -4 8 5 -2 0 6 4 0 | 1 |
За любознателните
Задача 17
В автомобилите, за комуникация между всички електронни компоненти се използва Controller Area Network bus. Различни устройства се свързват в една мрежа и си комуникират помежду си.
Единичен трансфер на данни се нарича "frame". Всеки "frame" следва стандартен формат, описващ какви данни се пренасят, колко и т.н. Как изглежда този формат може да намерите на: https://en.wikipedia.org/wiki/ISO_15765-2
От входа получавате осем 8-битови числа. Те представляват един CAN frame. Трябва да изкарате типа на frame-а, допълнителна информация ако има такива (като индекс при consecutive frame) и накрая самите данни.